Najprostsza wróżba
Wojciech Dindorf
Elżbieta Krawczyk


Jeśli czasem uczeń powinien przynieść podręcznik do szkoły, to na tę lekcję na pewno. Można tekst poniżej potraktować jak scenariusz lekcji (90 minut!) i krok po kroku czytać, odpowiadać na pytania, dyskutować i nawet wykonać doświadczenie z wahadełkiem na wózku (rys. 3) albo na deskorolce. Analiza wykresu (rys. 4) wykonanego "od środka" pojazdu jest, naszym zdaniem, bardzo pouczająca.

*********************************

Najprostsza wróżba
        Mamy do dyspozycji pojazd, o którym wiemy, że potrafi jechać tylko w jednym kierunku i z niezmienną prędkością v. W chwili, gdy pojazd ten znajdował się w obranym przez nas miejscu - nazwijmy je początkiem układu odniesienia - włączyliśmy stoper. Nasze przewidywanie będzie polegało na określeniu, jak daleko od tego miejsca znajduje się pojazd w dowolnej chwili. Stosujemy prosty "wzór przewidywacza".
        Po czasie t sekund nasz pojazd przejechał vt metrów. Jeśli tę odległość oznaczymy symbolem s, to możemy napisać:

s = vt

        Posłużmy się przykładem: niech nasz pojazd potrafi jechać z prędkością 5 m/s. Przeczytaj jeszcze raz: pięć metrów na sekundę. Co to znaczy? To znaczy, że w dwie sekundy potrafi przejechać 10 metrów (5 ˇ 2), w trzy - piętnaście (5 ˇ 3), w t sekund vt metrów. Dla dowolnie wybranego czasu potrafimy w ten sposób "przewidzieć", jak daleko od określonego miejsca będzie pojazd, jeśli przez cały czas się od nas oddalał (stała prędkość oznacza, według umowy, także stały kierunek ruchu, bo v jest wektorem). Można też przewidzieć, ile czasu musi upłynąć, by nasz pojazd dotarł do wybranego miejsca. Wtedy skorzystamy z tego samego wzoru zapisanego w innej formie:

t = s/v

        Odpowiedzmy na pytanie: Jak daleko od miejsca "startu" był pojazd po godzinie? Podstawmy wartości do wzoru s = vt =5 m/s o 3600 s = 18 000 m, czyli odpowiedzią na nasze pytanie jest 18 km. Na pytanie: Jak długo trwał przejazd odległości 2 cm?" odpowiemy po podstawieniu do wzoru wartość t = s/v, czyli t = 0,02/5 = 0,004 oczywiście sekund, rachunek na jednostkach możesz wykonać samodzielnie. 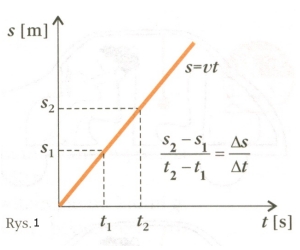Ruch pojazdu możemy zilustrować wykresem s (oś Y) jako funkcji t (oś x) (rys. 1). Jest to wyidealizowana sytuacja - gładko, równo, bez przyspieszeń pojazd sunie przed siebie i jest coraz dalej od nas. Najwygodniej jest, gdy za miejsce, w którym obiekt był w chwili włączenia stopera, obierze się początek układu odniesienia.
        Średnia prędkość pojazdu w dowolnym przedziale czasu przedstawia tu nachylenie prostej do osi czasu v = δs/δt.
        Wszystko, o czym przez dobrą chwilę czytasz, jest ci znane. Rozwiązywałeś wiele podobnych zadań w gimnazjum. Sporządzałeś wykresy, wyznaczałeś nachylenie prostej. Po tej rozgrzewce łatwo sobie przypomnisz, że wiesz więcej na ten temat. Wiesz, że jeśli szybkość nie jest stała, a rośnie równomiernie, tak jak w ruchu jednostajnym równomiernie wzrastała od-ległość, wykres zmian szybkości v w czasie t będzie kształtem przypominał wykres poprzedni, a jego nachylenie δs/δt będzie miarą średniej wartości przyspieszenia a:

a = δv/δt

       Przypomnę o tym, jak w ruchu prostoliniowym jednostajnie przyspieszonym - rozpoczynanym od stanu spoczynku - wyrażamy prędkość (szybkość) v w każdej chwili t:

v = at

zaś odpowiadającą chwili t odległość s od miejsca, skąd ruch (i pomiar czasu) rozpoczęto:

s = 1/2 at2

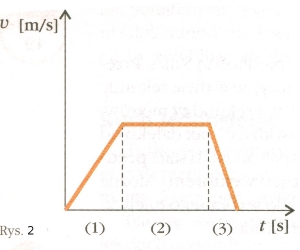
       Spróbuj teraz przeanalizować ze mną wykres zależności szybkości od czasu w ruchu, w którym można było wyróżnić wspomniane wyżej elementy: rozpędzanie się, jazda ze stałą prędkością i hamowanie (rys. 2).
       Jadąc kiedyś tramwajem do pracy, zastanawiałem się, jak wyglądałby wykres szybkości tramwaju, przedstawiony w zależności od czasu. Musiałby to być dość skomplikowany obraz.
        Wiem, że kierowcy autobusów, a nawet i niektórzy kierowcy ciężarówek (tak zwanych TIR-ów) mają wmontowane urządzenia, które takie wykresy wykonują. Pociągi również są wyposażone w urządzenia tego typu. Wykresy te, zapisywane w tak zwanej "czarnej skrzynce", są odczytywane tylko wtedy, gdy zachodzi konieczność sprawdzenia prawidłowości zachowania się kierowcy oraz szybkości pojazdu. W czarnych skrzynkach samolotów zapisywane są wszystkie parametry ruchu.
        Spróbowałem -jako pasażer, a więc obserwator od wewnątrz - wykonać taki wykres dla przejazdu między dwoma przystankami. Czas przyspieszania, czas jazdy ze stałą prędkością i czas hamowania, można było, choć niezbyt precyzyjnie, ustalić. Pod oknem wisiał na plastikowej żyłce jakiś tygodnik. W czasie przyspieszania, jak i hamowania, wychylał się w kierunku przeciwnym niż kierunek jazdy. W czasie jazdy ze stałą prędkością wisiał pionowo, tak jak wtedy, gdy tramwaj stał na przystanku.
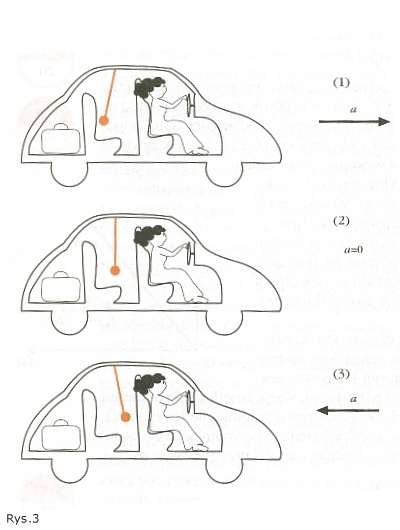
        Wahadełko zawieszone w każdym pojeździe służyć by mogło jako wskaźnik, a zawieszone na tle skali jako miernik przyspieszenia. Taki "przyspieszenioskop" (rys. 3) został pokazany w trzech różnych sytuacjach: w czasie przyspieszania, w czasie ruchu ze stalą prędkością i w czasie hamowania.
        Narysowałem wykres podobny do zamieszczonego na rysunku 2. Miałem wystarczająco dużo danych, aby oś czasu oznakować bez problemu, nie potrafiłem jednak określić, jaką wartość przypisać tej stałej maksymalnej prędkości, z którą tramwaj jechał przez zmierzone przeze mnie 31 sekund. Przy najbliższej okazji zrobiłem sobie spacer między tymi dwoma przystankami i w ten sposób mogłem w przybliżeniu ustalić, że odległość ta wynosi 1200 m. Wtedy już mogłem uzupełnić wykres (rys. 4).
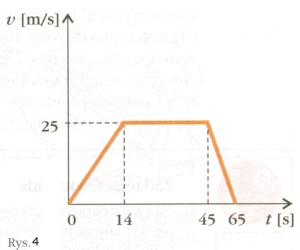
        Jak niektórzy zapewne pamiętają, drogę mierzy się tak, jakby mierzyło się pole powierzchni pod krzywą zależności prędkości od czasu. Jeśli ktoś nie pamięta, to na tym przykładzie spróbuję "ktosiowi" tę prawdę przybliżyć. Pole trapezu to połowa sumy podstaw pomnożona przez wysokość. Jasne? Dwa trójkąty plus prostokąt. Ale popatrzmy, tu podstawa ma wymiar czasu, wysokość ma wymiar ilorazu przemieszczenia przez czas, a zatem ich iloczyn da coś, co ma wymiar przemieszczenia. Coś, co się mierzy w metrach. Jeśli to coś miałoby wynosić 1200 m, to policzmy prędkość:

suma podstaw: 65 + 31 = 96 s, połowa sumy podstaw: 48 s,
więc v = 1200/48 = 25 m/s.

       A zatem ta największa prędkość tramwaju miałaby wynosić 25 m/s. Czemu nie? Łatwo policzyć (warto też zapamiętać), że l m/s = 3,6 km/h. Mój tramwaj rozpędził się do 90 km/h i "tak trzymał" przez 31 s, a potem przez 20 s hamował.
        A teraz proszę popatrzeć, ile jeszcze z takiego wykresu można się dowiedzieć, na przykład:
Jaką odległość przejechał tramwaj z największą prędkością?

s = vt, czyli s =25 m/s x 31 s = 775 m.

       Ile wynosiła droga hamowania? Średnia prędkość w czasie hamowania wynosiła 12,5 m/s, czas hamowania 20 s, droga hamowania == 12,5 x 20 = 250 m. Ile wynosiło przyspieszenie tramwaju? Przyspieszenie grawitacyjne na Ziemi g, wynosi, jak pamiętamy, blisko 10 m/s2. W naszym przypadku a = v/t (ponieważ v0= 0) czyli a = 25/14 =1,8 m/s2, równe 0,18g, co stanowi niewielką wartość w porównaniu na przykład z 5g rakiety wynoszącej Challengera na orbitę.
       Można by jeszcze policzyć, na jak długiej drodze tramwaj się rozpędzał, ale to bardzo proste. Ile wynosiło przyspieszenie ujemne (podczas hamowania) - też łatwe zadanie. Zastanówmy się, czy nie można by było, nie wychodząc z pojazdu i nawet nie pytając o nic motorniczego, wykonać tego w pełni opisanego wykresu? Podpowiem: można. Wystarczyłaby kartka papieru w drobną kratkę. Papier ten mógłby posłużyć do dokonania dwóch pomiarów kąta odchylenia od pionu żyłki, na której wisiało czasopismo. Należałoby w tym celu kilkoma punktami zaznaczyć kierunek pionu i oba odchylenia: w czasie przyspieszania i hamowania.
        Ktoś bardzo dociekliwy mógłby popatrzeć na tabliczkę fabryczną i odczytać masę i wymiary wagonu. Mając te dane i wielkości poprzednio policzone, mógłby policzyć siłę potrzebną do rozpędzenia wagonu, ilość energii cieplnej wydzielonej przy hamowaniu, minimalną moc silnika i kilka innych ciekawych rzeczy, takich na przykład, jak ta: czy szczelnie zamknięty wagon utonąłby, gdyby wpadł do wody. Do rozwiązania takich i innych problemów potrzebna jest sprawność "fizyczna".

*********************************

Któreś z zadań poniżej można zadać do przemyślenia w domu.

Zad.1.
Na kartce papieru kratkowanego przedstaw wykres zależności prędkości od czasu dla dowolnie wybranego fragmentu ruchu. Może to być kilka pierwszych minut po wstaniu z łóżka, może to być ruch kropli deszczu na szybie okna w twoim pokoju, może to być ruch autobusu, którym dojeżdżasz do szkoły - od przystanku do przystanku. Niech z tego wykresu będzie można odczytać, czy to był ruch chaotyczny, czy przewidywalny. Jak długo trwała obserwacja? Ile wynosiła największa prędkość? Czy w czasie obserwacji obiekt się zatrzymał? Jak daleko przemieścił się obserwowany obiekt? Czy z otrzymanego wykresu można określić dalszy przebieg wydarzenia?

Co powinniśmy "wyegzekwować"?

Wymagane są następujące elementy wykresu:
1) tytuł (temat), np.: prędkość szacunkowa sanek ześlizgujących się z górki od startu do zatrzymania;
2) określenie osi współrzędnych: dla osi pionowej v [m/s], dla poziomej t [s];
3) zaznaczenie punktów pomiarowych (jeśli pomiar był zrobiony);
4) najbardziej prawdopodobny przebieg obserwowanego zdarzenia (linia nie musi przechodzić przez punkty "pomiarowe").
Można próbować uświadomić uczniom, że jeśli poważnie potraktowali to zadanie, to mogli doznać przyjemności w pokonywaniu trudności związanych z szacowaniem wielkości (powinni pamiętać, że nie wszystko musi się dać zmierzyć tak dokładnie, jak by sobie tego życzyli), w odkryciu tego, jak wiele informacji zawierać może poprawnie sporządzony wykres.

Jeśli w zadaniu l zamiast prędkością zajmiesz się przemieszczeniem, otrzymasz też ciekawe, a może nawet prostsze do wykonania zadanie. Spróbuj.

Zad.2.
Ważne zadanie: oczekujemy tutaj przede wszystkim tego, by uczeń odtworzył sytuacje i raz jeszcze sporządził wykres, ale tym razem w układzie współrzędnych δr-t, czyli przemieszczenia i czasu. Jeśli zechce zrobić to poprawnie, to postara się, by na obu wykresach skala czasu była taka sama. Nie oczekujemy, by każdy uczeń z własnej inicjatywy dopasował oba wykresy do siebie. Jeśli tak się stanie, to zadanie następne ignorujemy, jeśli nie, to proponujemy zadanie 3.

Mając przed sobą dwa własnoręcznie sporządzone wykresy, możesz spróbować odpowiedzieć na pytanie, czy - a jeśli tak, to jak- można sporządzić jeden z wykresów na podstawie drugiego.

Zad.3.
Przez dokonanie takiego "tłumaczenia" najlepiej opanowuje się odczytywanie informacji z wykresu. Przemieszczenie ma się tak zmieniać, jak wielkość pola pod krzywą prędkości. Nachylenie drugiej krzywej ma w każdej chwili odpowiadać wartościom odkładanym dla tej chwili na krzywej prędkości. Można skopiować na folii stronę z podręcznika i wskazać uczniom, jak mają się do siebie kolejne "pochodne" wykresy. Można każdemu uczniowi dać kopię i zadać kilka pytań w formie testu, pytając o kilka detali z przedstawionych 9 wykresów sporządzonych dla trzech wyidealizowanych sytuacji.

Uwaga.
Nad wykresem na rys. 4 oraz nad doświadczeniem, którego ten wykres dotyczy, warto przeprowadzić bardziej szczegółową dyskusję.
Niech uczniowie odpowiedzą na pytanie:
"Zastanów się, czy nie można by było narysować takiego wykresu, nie wychodząc z tramwaju i nawet nie pytając o nic motorniczego? "
Co tu trzeba zrobić? Koniecznie trzeba pokazać na lekcji (lub wyegzekwować od uczniów), jak na podstawie wychylenia wahadła można określić wielkość przyspieszenia pojazdu. Odpowiedź daje rysunek.


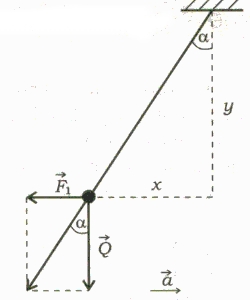
a = g (x/y)

F1 = ma
Q = mg

ma/mg = x/y



       Gdy pojazd startując przyspiesza, to mierząc kąt a i czas trwania ruchu przyspieszonego można określić maksymalną szybkość, a zatem i długość drogi. Można podobnie obliczyć, ile wynosiło przyspieszenie ujemne podczas hamowania.
        A jadąc ruchem jednostajnym? Co można zrobić, by określić odległość przejechaną w czasie, gdy wahadło wisiało pionowo? W przypadku jazdy pociągiem można by liczyć słupki kilometrowe i mierzyć czas. W tramwaju sprawa jest trudniejsza i może się nie obejść bez zaglądnięcia motorniczemu przez ramię i odczytaniu szybkości z tachometru. Czas jazdy też trzeba wyznaczyć. Najprościej oczywiście ilość kilometrów odczytać z miernika, ale to już żadna frajda (chyba, że chcemy sprawdzić, czy nasz pomiar był rzetelny).

Test pięciominutowy przygotowany dla każdego ucznia na małej kartce.
Dokończ następujące zdanie:
Na rysunku 3 walizka jest przymocowana do podłogi...
Propozycja odpowiedzi:
Na rysunku 3 walizka jest przymocowana do podłogi, ponieważ nie oparta o nic walizka nie przemieszcza się ani w tył przy przyspieszaniu auta, ani w przód przy hamowaniu. Fryzura kobiety-kierowcy jest też, jak widać, raczej usztywniona.


Wersja do druku


do góry