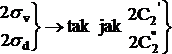Spektroskopia Ramana - drgania i widmo rozpraszania
Adrian Kamiński, Instytut Fizyki UAM
I. Czym jest spektroskopia ramanowska
Spektroskopia Ramana jest istotną metodą badania widm rotacyjnych i oscylacyjnych cząsteczek. Światło rozpraszane ma inne częstości niż światło padające. Obserwujemy
przesunięcie linii zarówno w stronę większych jak i mniejszych częstości, a tym samym większych i mniejszych energii. Kilka cech tej spektroskopii jest niezwykle ważnych. Jedną z nich jest możliwość użycia światła widzialnego do badania
widma Ramana. Potrafimy lepiej operować właśnie takim światłem w warunkach doświadczenia niż światłem podczerwonym lub mikrofalami. Niektóre dwuatomowe cząsteczki jak H2 czy O2 nie posiadają momentu dipolowego i dlatego nie są aktywne w
podczerwieni, a ich widma mogą być badane właśnie w widmie Ramana. Zatem np. pod tym względem spektroskopia ramanowska jest dopełnieniem spektroskopii
w podczerwieni i odwrotnie. Poza tym spektroskopia ramanowska umożliwia badanie ruchu cząsteczek, które zmieniając swoje położenie, wykonują np. ruchy obrotowe, co z kolei powoduje zmianę ich ukierunkowania
względem padającego promieniowania. Objawia się to zmianą polaryzacji w stosunku do światła padającego. Ponadto rozpraszanie Ramana, podobnie jak spektroskopia w podczerwieni, dostarcza informacji o budowie cząsteczki, wiązaniach międzyatomowych,
które ją tworzą, a także o ich polaryzowalności. Pozwala to przewidzieć reaktywność chemiczną i przebieg reakcji chemicznych.
II. Zjawisko Ramana - wgląd matematyczny
Jeżeli światło o natężeniu 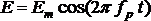 , (gdzie fp - częstotliwość promieniowania padającego, Em - wartość maksymalna natężenia) pada na cząsteczkę, to wystąpi oddziaływanie pomiędzy wektorem E,
a elektronowymi powłokami atomów tworzących cząsteczkę. Elektrony w cząsteczkach wykazują polaryzowalność α, czyli zdolność przemieszczania się
pod wpływem pola elektrycznego. W wyniku takiego przemieszczenia jest indukowany w cząsteczce moment dipolowy
, (gdzie fp - częstotliwość promieniowania padającego, Em - wartość maksymalna natężenia) pada na cząsteczkę, to wystąpi oddziaływanie pomiędzy wektorem E,
a elektronowymi powłokami atomów tworzących cząsteczkę. Elektrony w cząsteczkach wykazują polaryzowalność α, czyli zdolność przemieszczania się
pod wpływem pola elektrycznego. W wyniku takiego przemieszczenia jest indukowany w cząsteczce moment dipolowy
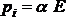 =
= 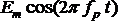 (1)
(1)
który oscyluje z częstością fp, co spowoduje emisję promieniowania o tej samej częstości, które nosi nazwę rozpraszania Rayleigha.
Jeżeli cząsteczka wykonuje drgania z częstością fosc, to zmienia się odległość r między atomami:
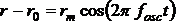 (2)
(2)
r0 - położenie równowagi
rm - maksymalne wychylenie,
Amplituda oscylacji indukowanego momentu dipolowego jest modulowana z częstością fosc, z jaką drga cząsteczka, a polaryzowalność zmienia się wraz z odległością r i może być przedstawiona w postaci szeregu potęgowego:
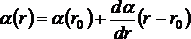 (3)
(3)
Wyrazy wyższych rzędów zostały pominięte. Biorąc pod uwagę wzory (2) i (3) oraz wzór E = Emcos(2πfpt), określający natężenie pola elektrycznego padającego światła, możemy przedstawić moment dipolowy:
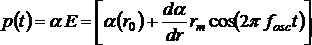 (4)
(4)
lub korzystając ze wzoru na iloczyn cosinusów:
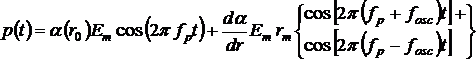 (5)
(5)
Argumenty funkcji cosinus zawierają częstotliwość światła padającego fp zmienioną o ± fosc. Oznacza to, że w widmie światła rozproszonego będziemy obserwować pasma o częstotliwościach fp ± fosc. Wielkość przesunięcia jest cechą charakterystyczną danej cząsteczki. Linie widma przesunięte w stronę mniejszych energii, są to tzw. pasma stokesowskie,
a w stronę większych energii - antystokesowskie. Pokazuje to rys.1. Zjawisko to nosi nazwę rozpraszania Ramana.
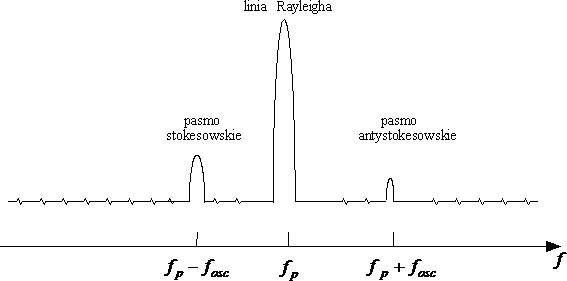
Rys. 1. Schemat widma ramanowskiego
III. Czynniki warunkujące zaistnienie zjawiska
Warunkiem zaistnienia zjawiska Ramana są zmiany polaryzowalności cząsteczki w trakcie danego drgania. Polaryzowalność jest wielkością, którą można wyrazić za pomocą tensora, który jest układem 9 współczynników (6)
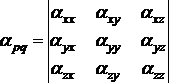 (6)
(6)
Gdy mówimy np. o zaindukowanym momencie dipolowym, to pierwszy wskaźnik dwuelementowego indeksu oznacza kierunek momentu dipolowego, a drugi kierunek przyłożonego pola elektrycznego (wektora natężenia pola). Składowe tensora polaryzowalności (STP) 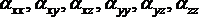 przekształcają się odpowiednio jak iloczyny współrzędnych x2, xy, xz, y2, yz oraz z2. Omówione w artykule "Symetria cząsteczki a aktywność widmowa jej drgań" (patrz Fizyka w Szkole nr 2, 2008) operacje symetrii cząsteczki i charaktery reprezentacji, posłużą nam również do określenia matematycznie,
kiedy dane drganie wnosi wkład do rozpraszania Ramana. Jeżeli charaktery reprezentacji drgania o danym typie symetrii są takie same jak STP, to drganie to jest aktywne w widmie ramanowskim. Zbadamy to
na przykładzie cząsteczki o trójkątnej strukturze przestrzennej typu woda oraz czworokątnej typu tetrametylocyklobutan.
przekształcają się odpowiednio jak iloczyny współrzędnych x2, xy, xz, y2, yz oraz z2. Omówione w artykule "Symetria cząsteczki a aktywność widmowa jej drgań" (patrz Fizyka w Szkole nr 2, 2008) operacje symetrii cząsteczki i charaktery reprezentacji, posłużą nam również do określenia matematycznie,
kiedy dane drganie wnosi wkład do rozpraszania Ramana. Jeżeli charaktery reprezentacji drgania o danym typie symetrii są takie same jak STP, to drganie to jest aktywne w widmie ramanowskim. Zbadamy to
na przykładzie cząsteczki o trójkątnej strukturze przestrzennej typu woda oraz czworokątnej typu tetrametylocyklobutan.
IV. Cząsteczka wody - aktywność w widmie Ramana
A. Składowe tensora polaryzowalności - prostokątny układ współrzędnych
Zobaczmy jak zmieniają się współrzędne dla operacji symetrii H2O, co
umożliwi określenie iloczynów współrzędnych, a tym samym STP. Dla tożsamości E żadna ze współrzędnych się nie zmienia, a więc składowymi są same +1 (pierwsza kolumna tabeli 1). Przy obrocie o 1800 C2 współrzędna x oraz y zmieniają znaki na przeciwne, a współrzędna z nie.
Po przemnożeniu przez siebie otrzymujemy składowe tensora (druga kolumna Tab.1), itd.
| |
E |
C2 |
σh |
σv |
| αxx |
1 |
1 |
1 |
1 |
| αxy |
1 |
1 |
-1 |
-1 |
| αxz |
1 |
-1 |
1 |
-1 |
| αyy |
1 |
1 |
1 |
1 |
| αyz |
1 |
-1 |
-1 |
1 |
| αzz |
1 |
1 |
1 |
1 |
Tab.1 Składowe tensora polaryzowalności dla H2O
B. Składowe tensora polaryzowalności - sferyczny układ współrzędnych
Związek pomiędzy współrzędnymi sferycznymi r, θ, φ i kartezjańskimi x, y, z punktu P przedstawia rys.2
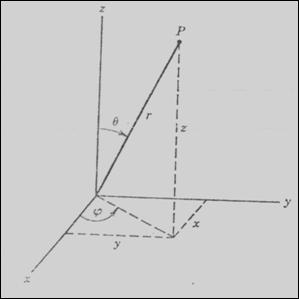
Rys.2. Współrzędne sferyczne r, θ, φ punktu P
i jego współrzędne prostokątne x, y, z
Algebraiczna postać tego związku jest następująca:
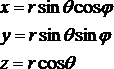 (7)
(7)
Przy operacjach symetrii r, θ nie zmieniają się, a tym samym nie zmieniają się również sinθ, cosθ - należy je traktować jako stałe. Odpowiednie iloczyny współrzędnych, a tym samym STP przekształcają się w następujący sposób:
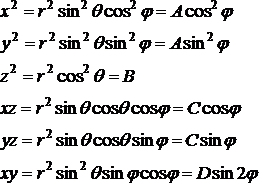 (8)
(8)
A, B, C, D - stałe.
W związku z tym patrzymy jak zmienia się kąt φ i odpowiednie iloczyny współrzędnych - wzory (8). Cząsteczka jest w płaszczyźnie xz. Dla operacji C2 kątem jest oczywiście 1800, przy operacjach odbicia σh, σv, obserwujemy zmianę kąta i jest to nasz kąt φ. Dla iloczynów x2, y2, z2 obieramy jakiś punkt odpowiednio na osi x, y, z, a dla iloczynów xy, xz, yz, punkt na płaszczyźnie odpowiednio xy, xz, yz i dokonujemy przekształceń zgodnie z operacjami symetrii.
Jeżeli w wyniku operacji znak funkcji się nie zmienia, to odpowiedni iloczyn współrzędnych, a tym samym STP jest równa +1. W przeciwnym wypadku -1. Oczywiście iloczyny x2, y2, z2 dają składowe tensora zawsze równe +1, ponieważ funkcje sinus i cosinus są w kwadracie (gdyby nawet zmienił się znak funkcji, to po podniesieniu do kwadratu będzie dodatnia), a przy z2 mamy stałą, czyli automatycznie składowa jest równa +1. Prześledźmy jak można otrzymać STP αxz. Umieszczamy punkt w płaszczyźnie xz, najlepiej na osi x, bo jest to wówczas najbardziej widoczne.
Tożsamość E niczego nie zmienia, więc składowa jest +1. C2 daje cos1800 = -1, odbicie σh zachowuje kąt nie zmieniony, a więc cos00 = 1, odbicie σv (w płaszczyźnie yz ) powoduje przejście punktu na ujemną część osi x, a tym samym kąt φ = 1800, czyli cos1800 = -1. Otrzymaliśmy STP αxz - Tab.1. Gdybyśmy chcieli otrzymać STP αxy, to obieramy punkt - jak było powiedziane - w płaszczyźnie xy, w połowie między osią x i y. Mamy zatem φ = 450. Dla poszczególnych operacji symetrii otrzymujemy:
C2 prowadzi do kąta 2250, σh: -450, σv: 1350. Mnożymy otrzymane kąty przez 2, bo przy iloczynie xy mamy 2φ, co daje - C2: 4500, σh: -900, σv: 2700. A więc:
C2: sin4500 = sin900 = 1
σh: sin(-900) = -sin900 = -1
σv: sin2700 = -1
E: brak zmiany znaku, czyli 1
Jest to zgodne ze STP z Tab.1. Analogicznie otrzymujemy pozostałe STP. Tak więc podejście oparte na przestrzennym układzie współrzędnych, daje te same wyniki w odniesieniu do możliwości znajdowania STP, co zastosowanie kartezjańskiego układu współrzędnych.
C. Iloczyn prosty reprezentacji a aktywność widmowa drgań w
rozpraszaniu Ramana
Znając charaktery reprezentacji możemy znaleźć charakter reprezentacji γ12, będącej tzw. iloczynem prostym reprezentacji γ1 i γ2. Jest on po prostu równy iloczynom charakterów reprezentacji γ1 i γ2 obliczonym oddzielnie dla każdej operacji symetrii należącej do danej grupy punktowej.
Tabela 2 podaje iloczyny proste reprezentacji dla cząsteczki wody.
| |
E |
C2 |
σh |
σv |
|
E |
C2 |
σh |
σv |
|
E |
C2 |
σh |
σv |
| A1 |
1 |
1 |
1 |
1 |
A1 |
1 |
1 |
1 |
1 |
A1 |
1 |
1 |
1 |
1 |
| A2 |
1 |
1 |
-1 |
-1 |
B1 |
1 |
-1 |
1 |
-1 |
B2 |
1 |
-1 |
-1 |
1 |
| A1 x A2 |
1 |
1 |
-1 |
-1 |
A1 x B1 |
1 |
-1 |
1 |
-1 |
A1 x B2 |
1 |
-1 |
-1 |
1 |
| |
E |
C2 |
σh |
σv |
|
E |
C2 |
σh |
σv |
| A2 |
1 |
1 |
-1 |
-1 |
A2 |
1 |
1 |
-1 |
-1 |
| B1 |
1 |
-1 |
1 |
-1 |
B2 |
1 |
-1 |
-1 |
1 |
| A2 x B1 |
1 |
-1 |
-1 |
1 |
A2 x B2 |
1 |
-1 |
1 |
-1 |
Tab.2. Iloczyny proste reprezentacji - cząsteczka H2O
Tworzymy teraz iloczyny proste posługując się tabelą 1 STP. Gdy w wyniku otrzymujemy reprezentację jednostkową (która odpowiada typowi symetrii A1), to dane drganie jest aktywne w widmie Ramana - wyrażenia (9).
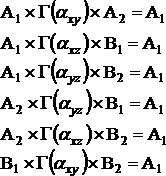 (9)
(9)
Czyli dla H2O drgania wszystkich typów symetrii są aktywne w widmie Ramana. Do takich samych wniosków można dojść szybciej porównując charaktery reprezentacji H2O i STP z tabeli 1. Jeżeli są takie same, to drganie daje wkład do rozpraszania Ramana. Np. wiersz drugi tab.1 jest taki sam jak charaktery reprezentacji typu symetrii A2, co oznacza, że drganie odpowiadające temu typowi jest aktywne. Możemy to zapisać:
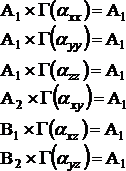 (10)
(10)
Drgania w pełni symetryczne, czyli mające reprezentację złożoną z samych +1, są spolaryzowane. Do drgań spolaryzowanych należy to o typie symetrii A1. Pozostałe drgania aktywne w widmie Ramana dają pasma zdepolaryzowane.
V. Tetrametylocyklobutan - widmo rozpraszania Ramana
Tetrametylocyklobutan (C8H8) jest cząsteczką złożoną z 8 atomów węgla i 8 atomów wodoru. Kształt przestrzenny i wiązania między atomami przedstawia rys.3.
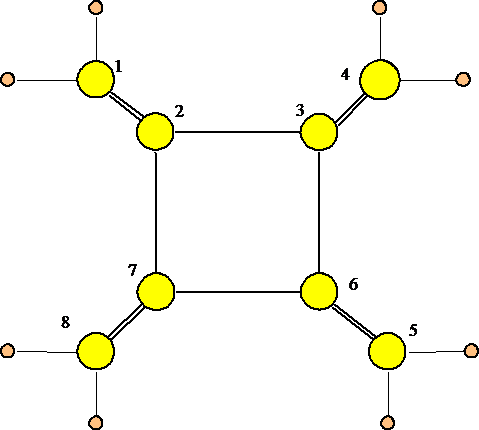
Rys.3. Tetrametylocyklobutan - żółte, duże kule - atomy węgla, mniejsze - atomy wodoru
Operacjami symetrii, które możemy wykonywać w przypadku C8H8 są: E, 2C4, C2, 2C2', 2C2", i, 2S4, σh, 2σv, 2σd.
Znajdźmy charaktery reprezentacji nieprzywiedlnych, w oparciu o przekształcenia prostej figury geometrycznej.
A. Otrzymywanie charakterów reprezentacji nieprzywiedlnych - metoda
wizualna
Symetria tetrametylocyklobutanu jest symetrią kwadratu z symetrycznymi "odgałęzieniami" odchodzącymi od wierzchołków. Dlatego, w celu znalezienia charakterów, zastosujemy kwadrat. Zasada jest podobna do tej zastosowanej w opracowaniu "Symetria cząsteczki, a aktywność widmowa jej drgań" [3], gdzie rozważane były wizualne metody otrzymywania charakterów reprezentacji nieprzywiedlnych dla cząsteczek H2O i NH3, w oparciu odpowiednio o prostokąt i trójkąt. Poniżej przedstawione są różne formy kwadratów z odpowiednim przypisaniem znaków, których przekształcanie prowadzi do otrzymania charakterów reprezentacji nieprzywiedlnych różnych typów symetrii. Dla drgań niezdegenerowanych - jeżeli figura w wyniku operacji przechodzi w siebie, to przypisanie jest +1,
w przeciwnym wypadku -1. Dla drgań zdegenerowanych przypisanie liczbowe jest podane we wzorach (11), (12).
1. Drgania zdegenerowane
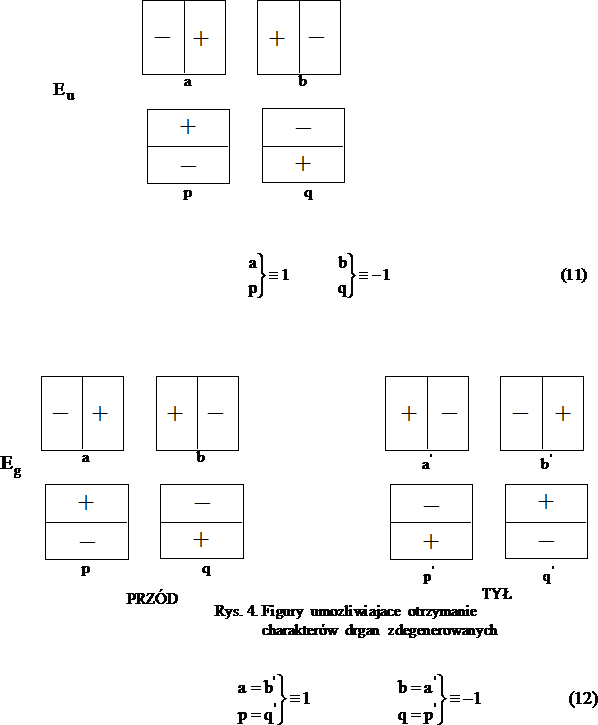
2. Drgania niezdegenerowane
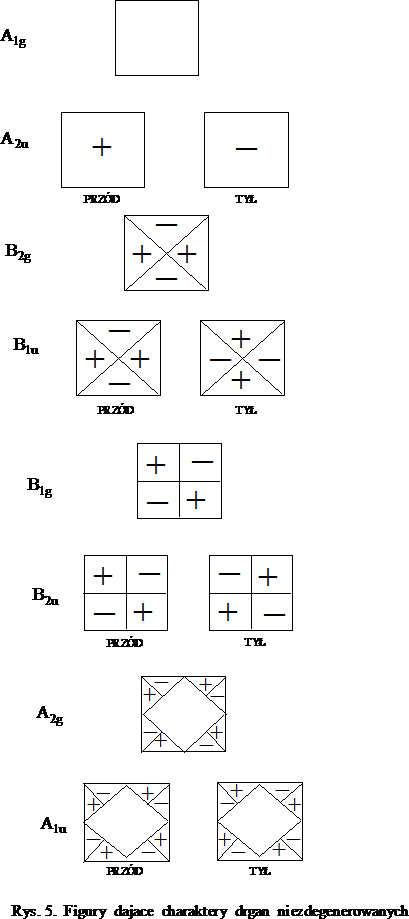
W przypadku drgań zdegenerowanych mamy dwie grupy figur: a, b i p, q. Wybieramy po jednej figurze z grupy np. a, p lub b, q i przekształcamy każdą z nich zgodnie z operacjami symetrii. Wyniki liczbowe (patrz (11), (12)) każdej z operacji dodajemy do siebie otrzymując charakter danego drgania zdegenerowanego. Ostatecznie tablica charakterów przedstawia się następująco (Tab.3):
| |
E |
2C4 |
C2 |
2C2' |
2C2" |
i |
2S4 |
σh |
2σv |
2σd |
|
|
| A1g |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x2 + y2, z2 |
| A2g |
1 |
1 |
1 |
-1 |
-1 |
1 |
1 |
1 |
-1 |
-1 |
Rz |
|
| B1g |
1 |
-1 |
1 |
1 |
-1 |
1 |
-1 |
1 |
1 |
-1 |
|
x2 - y2 |
| B2g |
1 |
-1 |
1 |
-1 |
1 |
1 |
-1 |
1 |
-1 |
1 |
|
xy |
| Eg |
2 |
0 |
-2 |
0 |
0 |
2 |
0 |
-2 |
0 |
0 |
(Rx, Ry) |
(xz, yz) |
| A1u |
1 |
1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
|
|
| A2u |
1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
1 |
1 |
z |
|
| B1u |
1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
-1 |
1 |
|
|
| B2u |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
|
|
| Eu |
2 |
0 |
-2 |
0 |
0 |
-2 |
0 |
2 |
0 |
0 |
(x,y) |
|
Tab.3. Charaktery reprezentacji nieprzywiedlnych tetrametylocyklobutanu
B. Zmiany elementów tensora polaryzowalności oraz ich kombinacji
liniowych
Oprócz podanych w wyrażeniach (8) iloczynów współrzędnych możemy określić również ich kombinacje liniowe i pary złożone np. z takiej kombinacji i iloczynu współrzędnych. Kombinacją liniową będą np. wyrażenia postaci x2 + y2 lub x2 - y2. Zobaczmy jaką mają one postać we współrzędnych sferycznych.
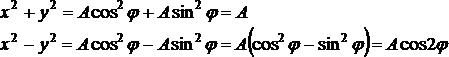 (13)
(13)
Posłużyliśmy się tutaj wyrażeniami (8). Możemy też stworzyć pary typu

Rozpatrzmy kombinację liniową współrzędnych x2 - y2, która zgodnie ze wzorem (13) jest równa Acos2φ. Dla uproszczenia pomińmy czynnik stały i sprawdźmy jakie wyniki otrzymamy przy przekształceniach przez poszczególne operacje symetrii cząsteczki tetrametylocyklobutanu. Jeżeli przy operacji znak funkcji cosinus nie ulega zmianie, wówczas kombinacja
x2 - y2 określana jest jako +1. W przypadku przeciwnym -1. Otrzymujemy w ten sposób cyfry odwzorowujące zmianę kombinacji współrzędnych x2 - y2 (zmiana kombinacji liniowej składowych tensora polaryzowalności), a jednocześnie cyfry z wiersza odpowiadającego typowi symetrii B1g tabeli charakterów (Tab.3). Dlatego, po pierwsze, zmianę kombinacji x2 - y2 umieszczamy we wspomnianym wierszu, a po drugie, iloczyn prosty 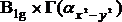 musi zawierać reprezentację jednostkową, bo
musi zawierać reprezentację jednostkową, bo 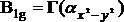 . Oznacza to, że drgania o typie symetrii B1g cząsteczki tetrametylocyklobutanu są aktywne w widmie Ramana. Dokładny opis otrzymywania składowych kombinacji x2 - y2,
iloczynu xy oraz pary (xz, yz) jest podany w załączniku.
. Oznacza to, że drgania o typie symetrii B1g cząsteczki tetrametylocyklobutanu są aktywne w widmie Ramana. Dokładny opis otrzymywania składowych kombinacji x2 - y2,
iloczynu xy oraz pary (xz, yz) jest podany w załączniku.
C. Liczba i rodzaj drgań tetrametylocyklobutanu aktywnych w
widmie Ramana
Stosując znany wzór (14), podany wcześniej w artykule Fizyka w szkole, "Symetria cząsteczki, a aktywność widmowa jej drgań" [3]
obliczmy liczbę translacji, rotacji i oscylacji danego typu symetrii.
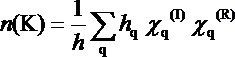 (14)
(14)
Znaczenie poszczególnych symboli jest następujące:
h - liczba wszystkich operacji symetrii rozpatrywanej cząsteczki
hq - liczba operacji symetrii w q- tej klasie. Klasa jest to zbiór operacji
symetrii, które mają te same charaktery. Np. klasa 2C4 w odniesieniu
do C8H8, to dwa obroty właściwe.
χq(I) - charakter reprezentacji nieprzywiedlnej (patrz Tab.3) q- tej klasy
χq(R) - charakter reprezentacji przywiedlnej [4] q-tej klasy
K - typ symetrii
By móc to zrealizować potrzebujemy reprezentację przywiedlną C8H8. Podaje ją tabela 4.
| |
E |
2C4 |
C2 |
2C2' |
2C2" |
i |
2S4 |
σh |
2σv |
2σd |
| l.n.p.s.a. |
16 |
0 |
0 |
4 |
0 |
0 |
0 |
16 |
4 |
0 |
| w.n.p.s.a.d.c. |
3 |
1 |
-1 |
-1 |
-1 |
-3 |
-1 |
1 |
1 |
1 |
| r.p. |
48 |
0 |
0 |
-4 |
0 |
0 |
0 |
16 |
4 |
0 |
Tab.4. l.n.p.s.a. - liczba nie przemieszczających się atomów
w.n.p.s.a.d.c. - wkład nie przemieszczających się atomów do charakteru [4]
r.p. - reprezentacja przywiedlna
n(A1g) = 1/16[1ˇ1ˇ48 + 2ˇ1ˇ0 + 1ˇ1ˇ0 + 2ˇ1ˇ(-4) + 2ˇ1ˇ0 + 1ˇ1ˇ0 + 2ˇ1ˇ0 + 1ˇ1ˇ16 +
2ˇ1ˇ4 + 2ˇ1ˇ0] = 4
n(A2g) = 1/16[1ˇ1ˇ48 + 2ˇ1ˇ0 + 1ˇ1ˇ0 + 2ˇ(-1)ˇ(-4) + 2ˇ(-1)ˇ0 + 1ˇ1ˇ0 + 2ˇ1ˇ0 +
1ˇ1ˇ16 + 2ˇ(-1)ˇ(-4) + 2ˇ(-1)ˇ0] = 5
Analogicznie:
n(B1g) = 4
n(B2g) = 4
n(Eg) = 5
n(A1u) = 1
n(A2u) = 3
n(B1u) = 1
n(B2u) = 3
n(Eu) = 8
Tak więc całkowita liczba translacji, rotacji, oscylacji:
γ = 4A1g + 5A2g +4B1g + 4B2g + 5Eg + A1u + 2A2u + B1u + 3B2u + 8Eu
Usuwając translacje i rotacje (kolumna 12 tabeli 3) otrzymamy liczbę i rodzaj oscylacji:
γosc = 4A1g + 4A2g +4B1g + 4B2g + 4Eg + A1u + 2A2u + B1u + 3B2u +7Eu
Chcąc znaleźć liczbę i rodzaj oscylacji aktywnych w widmie Ramana wybieramy te z tab.3, dla których zmienia się polaryzowalność - przynajmniej jedna składowa (kolumna 13 tabeli 3). Ostatecznie otrzymujemy:
γRAM = 4A1g + 4B1g + 4B2g + 4Eg
Zatem w widmie Ramana cząsteczki tetrametylocyklobutanu aktywne są 4 drgania A1g dające pasma spolaryzowane, bo pochodzą od drgań w pełni symetrycznych, czyli mających reprezentację nieprzywiedlną składającą się z samych +1. W widmie Ramana ponadto aktywne są 4 drgania B1g, 4 drgania B2g i 4 dwukrotnie zdegenerowane drgania Eg - wszystkie dające pasma zdepolaryzowane.
D. Wizualizacja drgań tetrametylocyklobutanu w widmie Ramana
Poniżej przedstawione są drgania aktywne w widmie Ramana cząsteczki C8H8. Symulacje komputerowe drgań cząsteczek o zbliżonych kształtach (a także innych) można oglądać na stronie www.fizmat.kki.pl oraz www.matphys.kki.pl



Rys.6. Drgania aktywne cząsteczki tetrametylocyklobutanu
w widmie Ramana
Cyfry stojące przy atomach węgla dla drgań o typie symetrii A1g i B1g oznaczają atomy cząsteczki tak jak przedstawiliśmy to na rys.3. Przy drganiach A1g pozostałe atomy wykonują takie same drgania, przy drganiach B1g, drgania zachodzą symetrycznie parami, tzn. atomy 3, 4, wykonują drgania takie same jak atomy 7, 8, a atomy 1, 2, takie same jak atomy 5, 6.
[1] P. Kowalczyk, Fizyka cząsteczkowa, Wydawnictwo Naukowe PWN, W - wa 2000.
[2] F.A. Cotton, Teoria grup - zastosowania w chemii, PWN, W - wa 1973.
[3] A. Kamiński, "Symetria cząsteczki, a aktywność widmowa jej drgań",
Fizyka w szkole, nr 2, 2008.
[4] Charaktery reprezentacji przywiedlnych oraz wkład nie przemieszczających się
są opisane na stronie: www.fizmat.kki.pl. Na tej stronie oraz na stronie:
www.physmat.kki.pl można prześledzić symulacje komputerowe drgań wielu
cząsteczek, w tym karbocyklicznych.
[5] R.L. Carter, Molecular Symmetry and Group Theory, J.Wiley&Sons, Nowy Jork
1997.
[6] G.M. Barrow, Introduction to Molecular Spectroscopy, Mc Graw - Hill, Nowy Jork
1962.
[7] A. Kamiński, Drgania normalne cząsteczek - aktywność widmowa i kierunki
wychyleń zrębów atomowych, Moja Fizyka nr 16, 2008.
ZAŁĄCZNIK
Zmiany kombinacji liniowych tensora polaryzowalności
Kombinacja x2 - y2 :
E - kąt φ się nie zmienia, więc +1
2C4 - φ = 900, ale mnożymy przez 2, bo jest 2φ, czyli mamy cos1800 = -1
φ = 2700, ale razy 2, czyli cos 5400 = cos (3600+1800) = cos 1800 = -1
C2 - φ = 1800, 2φ = 3600, cos 3600 = 1
2C2' - obrót względem osi "a" (rys.7) przekształca grupę atomów P o
1800, ale razy 2, czyli cos 3600 = 1. Przekształcenie względem osi
"b" daje ten sam punkt, czyli cos 00 = 1.
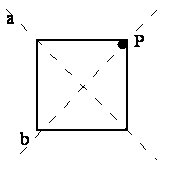
Rys. 7
2C2"- obrót względem osi "c" (rys.8) o 900, ale razy 2, czyli cos 1800= -1
Względem osi "d" obrót o -900, ale razy 2, czyli cos (-1800) =
= cos1800= -1
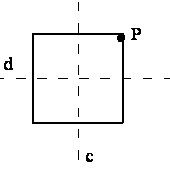
Rys. 8
Do tego samego wyniku dojdziemy traktując obroty 2C2', 2C2" jako sprzężone. Tzn. grupa atomów P - pierwsza ćwiartka, zostaje przekształcona o obrót o 900 względem osi "c" (rys.9), co daje drugą ćwiartkę P', gdzie cosinus jest ujemny, czyli C2" otrzymuje -1.
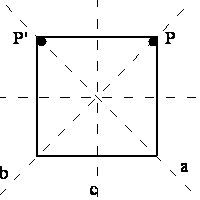
Rys. 9
Przekształcenie punktu P' względem osi "b" daje czwartą ćwiartkę, gdzie cosinus jest dodatni, a więc następuje zmiana znaku, czyli C2' otrzymuje +1. Podobnie możemy zrobić przekształcając najpierw względem "d", a następnie względem "b".
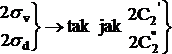
i - odpowiada kątowi 1800, ale razy 2, czyli cos (3600 + α). Znak się nie
zmienia, czyli +1.
2S4 - tak jak 2C4. Odbicie nie zmienia kąta φ.
σh - kąt 00, czyli mamy cos (00 + α). Znak się nie zmienia, czyli +1.
Iloczyn xy:
Iloczyn współrzędnych xy odpowiada we współrzędnych sferycznych
Dsin2φ. Pomijamy w rozważaniach stałą i obieramy jakiś punkt, dla którego φ jest różne od zera, najlepiej w I ćwiartce układu współrzędnych (kąt φ jest liczony w płaszczyźnie xy). Otrzymujemy następujące wyniki przekształceń przez poszczególne operacje symetrii:
E - kąt się nie zmienia, a tym samym znak funkcji sinus, więc
przypisanie +1
2C4 - sinus kąta φ dodatni - I ćwiartka (ewentualnie II - a, bo wartość
dodatnia jak wcześniej powiedziano) przechodzi w ujemną
- ćwiartka III (lub IV), bo φ = 900, ale razy 2, więc sin (1800 + α)
zmienia znak, więc przypisanie -1. Dla 2700 razy 2 mamy
sin (5400 + α), zmienia znak, więc -1.
C2 - φ = 1800, ale razy 2, czyli sin (3600 + α), znak się nie zmienia, więc
przypisanie +1.
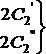 grupa atomów P z I ćwiartki zostaje przekształcona względem osi
"c" (rys.9.) o 900. W wyniku czego otrzymujemy P' z drugiej
ćwiartki, gdzie sinus jest dodatni, a więc dla C2" mamy +1.
Następnie P' zostaje przekształcony względem osi "b". Rezultatem
jest IV ćwiartka, gdzie sinus jest ujemny, czyli mamy -1.
grupa atomów P z I ćwiartki zostaje przekształcona względem osi
"c" (rys.9.) o 900. W wyniku czego otrzymujemy P' z drugiej
ćwiartki, gdzie sinus jest dodatni, a więc dla C2" mamy +1.
Następnie P' zostaje przekształcony względem osi "b". Rezultatem
jest IV ćwiartka, gdzie sinus jest ujemny, czyli mamy -1.
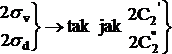
i - odpowiada kątowi 1800, ale razy 2, a więc sin(3600 + α) = sinα. Znak
się nie zmienia, czyli +1.
2S4 - tak jak 2C4. Odbicie nie zmienia kąta φ.
σh - kąt 00, czyli mamy cos (00 + α). Znak się nie zmienia, czyli +1.
Otrzymujemy w ten sposób cyfry odwzorowujące zmianę iloczynu współrzędnych xy, tym samym zmianę składowej tensora polaryzowalności αxy, co pokrywa się z cyframi wiersza odpowiadającego typowi symetrii B2g tabeli charakterów (Tab.3). Dlatego, mamy analogiczne wnioski jak przy kombinacji x2 - y2 , tzn. umieszczamy składową tensora w wierszu odpowiadającym B2g,
iloczyn prosty 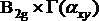 musi zawierać reprezentację jednostkową, bo
musi zawierać reprezentację jednostkową, bo 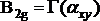 . Oznacza to, że drgania o typie symetrii B 2g cząsteczki tetrametylocyklobutanu są aktywne w widmie Ramana.
. Oznacza to, że drgania o typie symetrii B 2g cząsteczki tetrametylocyklobutanu są aktywne w widmie Ramana.
Para (xz, yz):
Przekształca się ona tak samo jak para strzałek (Rx, Ry) (rys.10).
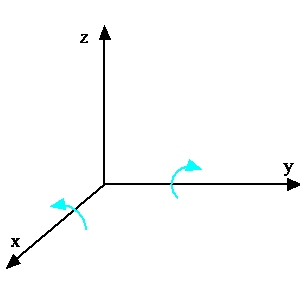
Rys. 10. Strzałki owinięte wokół osi x i y można przekształcać
I tak:
E - strzałki nie zmieniają swojego kierunku obrotu, więc dwa razy +1,
razem +2.
2C4 - obrót, stosujemy macierz obrotu 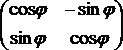 . Dla 900 ślad
macierzy Tr = 0, tak samo dla 2700, Tr = 0.
. Dla 900 ślad
macierzy Tr = 0, tak samo dla 2700, Tr = 0.
C2 - obrót o 1800, Tr = -2
2C2' - przekształcamy przez macierz odpowiadającą przekształceniu
względem osi "d" (rys.6) 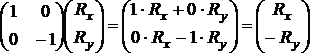 Tr (d) = 0
Tr (d) = 0
Dla osi "c" macierzą przekształcenia jest 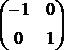 . Tr (c) = 0
. Tr (c) = 0
Tr (c) + Tr (d) = 0
2C2" - Weźmy jakiś punkt z I ćwiartki. Przekształcenie względem osi "b"
odpowiada macierzy 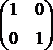 Tr (b) = 2. Przekształcenie względem
"a" odpowiada macierzy
Tr (b) = 2. Przekształcenie względem
"a" odpowiada macierzy 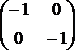 Tr (a) = -2. Ostatecznie:
Tr (a) + Tr (b) = 0
Tr (a) = -2. Ostatecznie:
Tr (a) + Tr (b) = 0
i - rozpatrujemy (Rx, Ry). Przekształcenie inwersji nie zmienia kierunku
obrotu zarówno Rx jak i Ry, a więc dwa razy +1, czyli razem +2.
σh - następuje zmiana kierunku obrotu strzałek, a więc dwa razy -1,
razem -2.
2S4 - tak jak 2C4
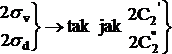
Otrzymujemy w ten sposób cyfry odwzorowujące zmianę pary (xz, yz), tym samym zmianę pary składowych tensora polaryzowalności (αxz, αyz). Pokrywa się to jednocześnie z cyframi wiersza odpowiadającego typowi symetrii Eg tabeli charakterów (Tab.3). Dlatego, parę (xz, yz) umieszczamy w wierszu odpowiadającym Eg, iloczyn prosty 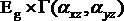 musi zawierać reprezentację jednostkową, bo
musi zawierać reprezentację jednostkową, bo 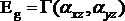 . Oznacza to, że drgania o typie symetrii Eg
cząsteczki tetrametylocyklobutanu są aktywne w widmie Ramana.
. Oznacza to, że drgania o typie symetrii Eg
cząsteczki tetrametylocyklobutanu są aktywne w widmie Ramana.
Wersja do druku 
do góry
![]() =
= ![]() (1)
(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)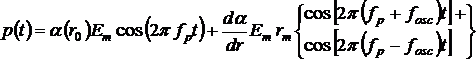 (5)
(5)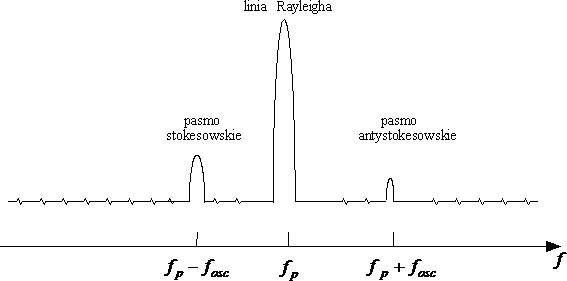
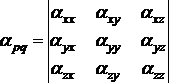 (6)
(6)
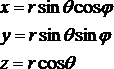 (7)
(7)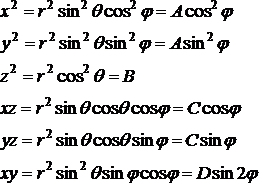 (8)
(8)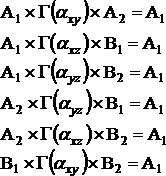 (9)
(9)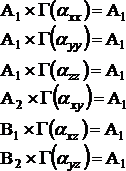 (10)
(10)


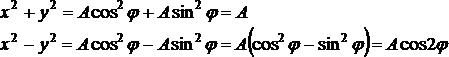 (13)
(13)
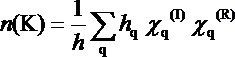 (14)
(14)





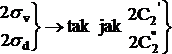
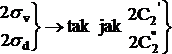

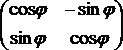 . Dla 900 ślad
macierzy Tr = 0, tak samo dla 2700, Tr = 0.
. Dla 900 ślad
macierzy Tr = 0, tak samo dla 2700, Tr = 0.
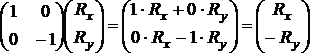 Tr (d) = 0
Tr (d) = 0
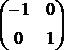 . Tr (c) = 0
. Tr (c) = 0
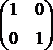 Tr (b) = 2. Przekształcenie względem
"a" odpowiada macierzy
Tr (b) = 2. Przekształcenie względem
"a" odpowiada macierzy 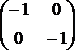 Tr (a) = -2. Ostatecznie:
Tr (a) + Tr (b) = 0
Tr (a) = -2. Ostatecznie:
Tr (a) + Tr (b) = 0